Простейшее объяснение парадокса монти холла
Содержание:
Разбор парадокса Монти Холла
Есть три варианта развития событий:
|
Дверь 1 |
Дверь 2 |
Дверь 3 |
Результат, если менять выбор |
Результат, если не менять выбор |
|
Авто |
Коза |
Коза |
Коза |
Авто |
|
Коза |
Авто |
Коза |
Авто |
Коза |
|
Коза |
Коза |
Авто |
Авто |
Коза |
Во время решения представленной задачи обычно приводятся такие рассуждения: ведущий в каждом случае убирает одну дверь с козой, следовательно, вероятность нахождения автомобиля за одной из двух закрытых дверей приравнивается к ½, независимо от того, какой выбор был сделан изначально. Однако это не так.
Смысл в том, что, делая первый выбор, участник разделяет двери на A (выбранную), B и C (оставшиеся). Шансы (P) на то, что машина стоит за дверью A, равны 1/3, а на то, что она за дверьми B и C равны 2/3. И шансы на успех при выборе дверей B и C вычисляются так:
P(B) = 2/3 * ½ = 1/3
P(C) = 2/3 * ½ = 1/3
Где ½ является условной вероятностью того, что машина находится именно за этой дверью, при условии, что машина не за той дверью, что выбрал игрок.
Ведущий, открывая заведомо проигрышную дверь из двух оставшихся, сообщает игроку 1 бит информации и изменяет тем самым условные вероятности для дверей B и C на значения 1 и 0. Теперь шансы на успех будут вычисляться так:
P(B) = 2/3*1 = 2/3
P(C) = 2/3*0 = 0
И получается, что если игрок изменит свой изначальный выбор, то его шанс на успех будет равен 2/3.
Объясняется это следующим образом: изменяя свой выбор после манипуляций ведущего, игрок выиграет, если изначально он выбрал дверь с козой, т.к. ведущий открывает вторую дверь с козой, а игроку остаётся лишь поменять двери. Выбрать же изначально дверь с козой можно двумя способами (2/3), соответственно, если игрок заменит двери, то выиграет с вероятностью 2/3. Именно из-за противоречия такого вывода интуитивному восприятию задача и получила статус парадокса.
Интуитивное восприятие говорит о следующем: когда ведущий открывает проигрышную дверь, перед игроком встаёт новая задача, на первый взгляд не связанная с изначальным выбором, т.к. коза за открываемой ведущим дверью будет там в любом случае, независимо от того, проигрышную или выигрышную дверь изначально выбрал игрок.
После открытия ведущим двери игрок должен снова сделать выбор – либо остановиться на прежней двери, либо выбрать новую. Это значит, что игрок делает именно новый выбор, а не меняет изначальный. И математическим решением рассматриваются две последовательные и связанные друг с другом задачи ведущего.
Но нужно иметь в виду, что ведущий открывает дверь именно из тех двух, которые остались, но не ту, что выбрал игрок. А значит, шанс на то, что машина находится за оставшейся дверью, увеличиваются, т.к. ведущий её не выбрал. Если же ведущий знает, что за выбранной игроком дверью стоит коза, всё-таки её откроет, он тем самым заведомо снизит вероятность того, что игрок выберет правильную дверь, ведь вероятность успеха станет равна ½. Но это уже игра по иным правилам.
А вот ещё одно объяснение: допустим, игрок играет по представленной выше системе, т.е. из дверей B или C всегда выбирает ту, что отличается от изначального выбора. Проиграет он в том случае, если изначально выбрал дверь с автомобилем, т.к. впоследствии выберет дверь с козой. В любом другом случае игрок выиграет, если изначально выбрал проигрышный вариант. Однако вероятность того, что изначально он выберет его, равна 2/3, из чего следует, что для успеха в игре сначала нужно сделать ошибку, вероятность которой в два раза больше вероятности правильного выбора.
Третье объяснение: представим, что дверей не 3, а 1000. После того как игрок сделал выбор, ведущий убирает 998 ненужных дверей – остаются только две двери: выбранная игроком и ещё одна. Но шанс на то, что машина за каждой из дверей совсем не ½. Скорее всего (0,999%) машина будет за той дверью, которую игрок не выбрал изначально, т.е. за дверью, отобранной из оставшихся после первого выбора 999 других. Примерно так же нужно и рассуждать при выборе из трёх дверей, пусть шансы на успех и снижаются и становятся 2/3.
И последнее объяснение – замена условий. Допустим, что вместо того, чтобы делать изначальный выбор, например, двери №1, и вместо открытия двери №2 или №3 ведущим, игрок должен сделать верный выбор с первого раза, если ему известно, что вероятность успеха с дверью №1 равна 33%, но об отсутствии машины за дверьми №2 и №3 он не знает ничего. Из этого следует, что шанс на успех с последней дверью будет составлять 66%, т.е. вероятность победы увеличивается вдвое.
Но каково будет положение дел, если ведущий станет вести себя иначе?
Решение задачи
Изначально нужно оговориться, что любые махинации исключены, автомобиль находится за одной и той же дверью время всего шоу. Никто не меняет его местоположение.
В самом начале шансы угадать машину за дверью равнялись 33.3%. После того, как ведущий открыл одну из дверей, остается всего две двери, а значит, шансы угадать автомобиль, казалось бы, повышаются – 50%. Но люди заблуждаются.
В реальности, игроки, которые меняют свое решение, выигрывают в 2 раза чаще, чем те, кто остаются верны своему выбору. На самом деле шансы игрока угадать правильную дверь после того, как ведущий открыл одну из дверей, остаются на том же уровне – 33.3%. В то же время, если поменять свой выбор, шансы на успех будут в два раза выше – 66.5%. Это может показаться бредом, однако, этому есть логическое объяснение.
Итак, вначале шанс угадать автомобиль был 33.3%. Пусть это будет дверь №1. Значит суммарная вероятность авто за дверями №2 и №3 – 66.5%. После того, как ведущий открыл одну из дверей, и там оказалась коза, очевидно, что шансы автомобиля за этой дверью равны 0%. Следовательно, эти 33.3% вероятности нахождения автомобиля за открытой ведущим дверью переносятся на тот выбор, который не сделал игрок, потому что общая вероятность нахождения авто за дверью – 100%, а шансы увидеть ее за дверями №2 и №3 осталась без изменений – 66.5%. Т.е. поменяв свое первоначальное решение, игрок в 2 раза повышает свои шансы на успех.
Личная жизнь [ править ]
28 сентября 1947 года Холл женился на Мэрилин Дорин Плоттель (17 мая 1927 — 5 июня 2017); их познакомил общий кузен Норман Шниер в прошлом году. Позже они стали гражданами США. У них было трое детей: актриса Джоанна Глисон, обладательница премии Тони ; Шэрон Холл Кесслер, президент Endemol Shine Studios; и Ричард Холл, Эмй выигрывающий телевизионный продюсер . Монти и Мэрилин жили в Беверли-Хиллз, Калифорния , с 1962 года до своей смерти; Мэрилин умерла на четыре месяца раньше своего мужа.
Смерть править
Холл умер от сердечной недостаточности 30 сентября 2017 года в своем доме в Беверли-Хиллз чуть более чем через месяц после своего 96-летия. 3 октября он был похоронен на кладбище в Мемориальном парке Хиллсайд .
Объяснение роста вероятности
В отличие от интуитивного уровня, где наше сознание рассматривает событие после смены ячейки как нечто отдельное и забывает о первоначальном выборе, математика не разрывает эти два события, а наоборот сохраняет цепочку событий от начала до конца. Итак, как мы ранее и говорили, шансы на выигрыш при попадании сходу на слиток у нас 1/3, а вероятность, что мы выберем ячейку с монетой 2/3 (поскольку у нас есть один слиток и две монеты).
Далее распишем все возможные случаи развития событий при условии вышеупомянутого классического поведения ведущего, в нашем случае банкира.
- Выбираем изначально банковскую ячейку со слитком — вероятность 1/3.
- Если игрок изменяет свой выбор, принимая предложение банкира, — он проигрывает.
- Если игрок не изменяет выбор, не принимая предложение банкира, — он выигрывает.
- Выбираем с первого раза банковскую ячейку с в монеткой — вероятность 2/3.
- Если игрок поменяет свой выбор — выиграл.
- Если игрок не изменяет выбор — проиграл.
Итак, для того, чтобы игрок ушел из банка со слитком золота в кармане, он должен выбрать изгначально проигрышную позицию с монеткой (вероятность 1/3), и после этого принять предложение банкира сменить ячейку.
Для того, чтобы понять данный парадокс и вырваться из оков шаблона первоначального выбора и оставшихся ячеек, давайте представим поведение игрока ровным счетом наоборот. Перед тем как банкир предложит ячейку для выбора, игрок мысленно точно определяется с тем, что он меняет свой выбор, и только после этого для него следует событие открытия лишней двери. Почему нет? Ведь открытая дверь не дает для него большей информации в такой логической последовательности. На первом этапе времени игрок разделяет ячейки на две разные области: первая — область с одной ячейкой с его первоначальным выбором, вторая с двумя оставшимися ячейками. Далее игроку предстоит сделать выбор между двумя областями. Вероятность достать из ячейки золотой слиток из первой области 1/3, из второй 2/3. Выбор следует за второй областью, в которой он может открыть две ячейки, первую откроет банкир, вторую он сам.
Существует еще более понятное объяснение парадокса Монти Холла. Для этого необходимо поменять формулировку задания. Банкир дает понять, что в одной из трех банковских ячеек находится золотой слиток. В первом случае он предлагает открыть одну из трех ячеек, а во втором — одновременно две. Что выберет игрок? Ну конечно сразу две, за счет повышения вероятности в два раза. И тот момент, когда банкир открыл ячейку с монеткой, это игроку на самом деле никак не помогает и не препятствует выбору, ведь банкир в любом случае покажет эту ячейку с монеткой, поэтому игрок может попросту игнорировать это действие. Со стороны игрока можно лишь только поблагодарить банкира за то, что он ему облегчил жизнь, и вместо двух ему пришлось открыть одну ячейку. Ну и окончательно можно избавится от синдрома парадокса если поставить себя на место банкира, который изначально знает, что игрок в двух из трех случаев указывает на неправильную дверь. Для банкира парадокс отсутствует как таковой, ведь он точно в такой инверсии событий уверен, что в случае смены событий игрок забирает золотой слиточек.

Парадокс Монти Холла явно не позволяет быть в выигрыше консерваторам, которые железобетонно стоят на своем первоначальном выборе и теряют свой шанс роста вероятности. Для консерваторов он так и останется 1/3. Для бдительных и рассудительных людей он вырастает до вышеуказанных 2/3.
Все приведенные утверждения актуальны лишь в соблюдении изначально оговоренных условий.
Карьера
Первая работа Холла на радио была радио в Виннипеге еще будучи студентом. Некоторое время он работал на Канадский совет по пшенице после окончания учебы, прежде чем принять решение о продолжении карьеры в сфере телевещания. Он переехал в Торонто в 1946 году и нашел работу на радиостанции ЧУМ, где руководство сократило его имя до Холла и неправильно написало его имя как «Монти» на рекламных щитах, что дало ему Сценический псевдоним «Монти Холл». В течение следующего десятилетия он вел и продюсировал ряд программ для радиостанций в Торонто, а также Кто я? на CFRB, который распространялся на национальном уровне в Канаде через частные объединения до 1959 года. У него также было несколько краткосрочных программ на CBC Television после того, как он был запущен в 1952 году, но когда они были отменены и у него отняли другую программу, которую он задумал, Холл решил, что у него нет будущего на канадском телевидении.
Зал переехал в Нью-Йорк в 1955 году, пытаясь проникнуть в американское вещание, но несколько раз в месяц ездил в Торонто, чтобы записывать блоки эпизодов Кто я? В Нью-Йорке Холл проводил игровые шоу, такие как Бинго дома на WABD-TV и гостевые более известные игровые шоу, такие как Преуспеть на CBS и на NBC. Он был ведущим / исполнителем двух местных телешоу для детей в Нью-Йорке. Ковбойский театр за WRCA (Канал 4) в 1956 г. и Веселье по утрам за WNEW (Гл. 5) в начале 1960-х гг. С 1956 по 1960 год, вместе с репортером NBC Radio Морганом Битти, Холл был одним из организаторов субботнего ночного сегмента программы выходного дня NBC Radio Network. Монитор с 20:00 до полуночи (EST). По крайней мере, две записи Холла на Монитор известно о существовании.
Холл был радиоаналитиком в Нью-Йорк Рейнджерс из Национальная хоккейная лига в сезоне 1959–1960 гг.
Он преуспел Джек Нарз как ведущий игрового шоу называется Видео Деревня, который транслировался с 1960 по 1962 год на канале CBS. С 1961 по 1962 год в Зале проходил Дополнительная выгода, Видео Деревня Джуниор, в котором участвовали дети. После переезда в Южная Калифорния, Холл стал ведущим игрового шоу Давайте сделаем сделку, который он разработал и продюсировал с партнером Стефаном Хатосом.Давайте сделаем сделку транслировался на NBC днем с 30 декабря 1963 г. по 27 декабря 1968 г. и далее ABC дневное время с 30 декабря 1968 года по 9 июля 1976 года, а также два показа в прайм-тайм. Он транслировался в синдикации с 1971 по 1977 год, с 1980 по 1981, с 1984 по 1986, и снова на NBC кратко с 1990 по 1991 год, с Холлом, заменившим Боб Хилтон, который был уволен. Он был продюсером или исполнительным продюсером шоу на протяжении большей части его тиражей. Во время первого показа шоу Холл появилась вместе с моделью. Кэрол Меррилл и диктор Джей Стюарт.
Помимо Давайте сделаем сделку, игровое шоу Доли секунды, который первоначально работал на ABC с 1972 по 1975 год с Том Кеннеди в качестве ведущего, и снова в синдикации в 1986 году с Холлом, ведущим эту версию, была единственной другой успешной программой от Hatos-Hall Productions. Включены и другие игровые шоу от продюсерской компании Hatos и Hall. Письмо счастья в 1966 г .; возрождение почтенной панельной викторины 1950-х годов, Маскарадная вечеринка в 1974 г .; Трое за деньги в 1975 г .; Это чья-то догадка в 1977 году, которые воссоединились Давайте сделаем сделку диктор Джей Стюарт с Холлом, который также вел шоу, и канадская Шутка над нами в 1983 г. Зал заполнялся в качестве приглашенного ведущего на нескольких дневных игровых шоу, пока Давайте сделаем сделку был на NBC, особенно Что это за песня? и PDQ.
В 1979 году Холл провел единственное игровое шоу с тех пор, как Видео Деревня чего он не производил, Гудсон-Тодманс . Также в 1979 году Холл появился на игровом шоу. Пароль Плюс как участник игрового шоу. Он появился как он сам в эпизоде »Кольцо обещаний» Шоу 70-х в 2001. Он играл ведущего конкурса красоты, который намеревался стать «самым влиятельным ведущим игрового шоу в мире» в мультсериале Disney. Американский дракон: Джейк Лонг. Он появился на GSN Live 14 марта 2008 г., и состоялась игра Давайте сделаем сделку за Доброе утро америка 18 августа 2008 г., в рамках недели Game Show Reunion.
Летом 2009 года CBS объявила о возрождении Давайте сделаем сделку в дневном расписании. Премьера шоу состоялась 5 октября 2009 года. Уэйн Брэди как хозяин. Холл считался «креативным консультантом» до своей смерти в 2017 году, и по-прежнему считается соавтором формата (со Стефаном Хатосом), а Hatos / Hall Productions — в качестве совместной производственной компании (с Фримантл).
Парадокс
Парадокс впервые был сформулирован американским математиком Стивом Селвином ещё в 1975 году, но широкую известность он приобрёл благодаря популярному игровому шоу «Давайте заключим сделку». В честь ведущего этой телевикторины, которого звали Монти Холл, парадокс и получил своё название.
В чём же суть парадокса Монти Холла?
Представьте, что перед вами три двери, как показано на рисунке ниже. За двумя дверьми находятся козы, за одной — автомобиль. Надо угадать дверь с автомобилем, и он ваш.

Казалось бы, ничего сложного. Но, как говорилось в одном фильме: «Если бы задача так просто решалась, то армянское радио этим бы не занималось». В своей передаче, после того как участник выбирал дверь, Монти всегда открывал одну из дверей с козой и предлагал ему поменять свой выбор. А вы поменяли бы или нет?
Этот вопрос многих ставит в тупик. Люди обычно думают: «Ну какая разница: остались две двери, и машина может с одинаковой вероятностью 50% оказаться как за одной, так и за другой дверью?». … И оказываются неправы. Правильный ответ — всегда менять первоначальный выбор. Поступая так, вы удваиваете свои шансы на победу.
Удивлены? Такой ответ для многих становится откровением: мало кто ожидает этого. Давайте подробно разберёмся, как так получается.
Итак, вы выбрали одну из трёх дверей. Вероятность того, что машина окажется именно за ней, составляет 1/3. А вероятность того, что она окажется за одной из двух оставшихся (то есть не выбранных вами) дверей, будет 2/3. Это должно быть понятно.
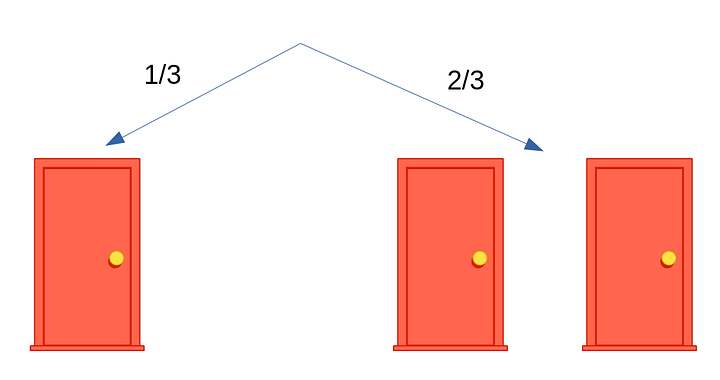
На рисунке у нас наглядно показаны эти вероятности: 1/3 слева и 2/3 справа.
Теперь Монти открывает одну из невыбранных дверей — тех, что справа. И открывает он всегда ту, за которой коза.
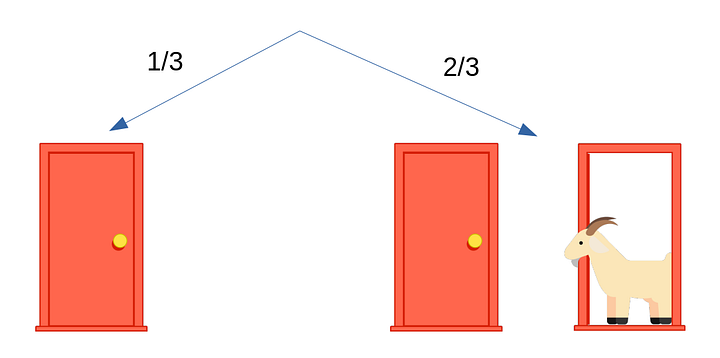
Вероятности остаются неизменными: 1/3 слева (ваш первоначальный выбор) и 2/3 справа. Изменилось лишь то, что справа одна дверь теперь открыта, но вероятность для оставшейся неоткрытой двери здесь та же, что была прежде для обеих.
Если не совсем понятно, попробуем объяснить на примере с десятью дверьми.

Выбранная вами дверь будет слева, остальные девять — справа (как на рисунке ниже). Вероятность того, что вы угадали дверь с машиной, будет 1/10. Вероятность того, что вы не угадали и машина окажется за одной из оставшихся девяти дверей, будет 9/10.
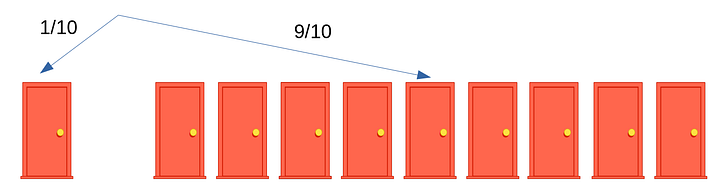
Дальше Монти открывает восемь из этих невыбранных девяти дверей, причем за всеми восемью — козы. Как поступить теперь: поменять свой выбор или нет? Конечно, поменять! Ведь теперь восемь из девяти дверей справа открыты, а вероятность того, что машина окажется за оставшейся девятой дверью (как мы уже посчитали ранее), равна 9/10.
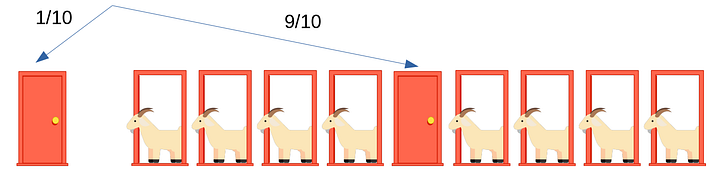
Ответ на вопрос станет ещё очевиднее, если представить, что Монти даёт вам возможность открыть не одну оставшуюся справа неоткрытой дверь, а сразу все девять!
Вот и всё
Это так просто! Однако важно не забывать, что всегда есть вероятность проигрыша. Верное решение определяется стратегией
Правильная стратегия — делать так, чтобы шансы на победу были максимальными или хотя бы такими, которые позволяют больше выигрывать, чем проигрывать.
Внешние ссылки [ править ]
- Монти Холл в IMDb
- Биография Монти на Letmakeadeal.com
- Профиль Монти Холла в цифровых архивах CBC (1970)
- Монти Холл в Find a Grave
- Монти Холл на интервью: устная история телевидения
| Предшественник None | Ведущий программы Let’s Make a Deal 1963–1986 | Преемник Боб Хилтон |
| Предшественник Джин Вуд | Ведущий Beat the Clock 1979–1980 | Преемник Гэри Крегера |
| Предшественник Том Кеннеди | Хозяин Split Second 1986–1987 | Ничего не удалось |
| Предшественник Боб Хилтон | Ведущий программы Let’s Make a Deal 1990–1991 | Преемник Билли Буша |
| vтеДневная премия «Эмми» за заслуги перед жизнью |
|---|
|
| Авторитетный контроль |
|
|---|
Ранние годы
Отпечатки ладоней Холла перед амфитеатром Голливуд-Хиллз в тематическом парке Disney World ‘s Disney’s Hollywood Studios.
Холл родился как Монте Халпарин в Виннипеге , Манитоба , 25 августа 1921 года в семье ортодоксальных евреев, родителей Мориса Харви Халпарина, владевшего бойней, и Роуз (урожденная Русен). Он вырос в северной части Виннипега, где учился в школе лорда Селкирка (Элмвуд, Виннипег), а затем и в средней школе Св. Иоанна . Холл получил степень бакалавра наук в Университете Манитобы , где он специализировался в области химии и зоологии . Он надеялся поступить в медицинский институт, но не был принят из-за секретных квот, ограничивающих количество принимаемых еврейских студентов .
Ссылки [ править ]
- ^ a b Алмэси, Стив; Марко, Тони. «Монти Холл, ведущий« Давай заключим сделку », умер в 96 лет» . CNN . Проверено 1 октября 2017 года .
- ^ a b c Холл, Монти; Либби, Билл (1973). Ведущий Монти Холл . Нью-Йорк: Гроссет и Данлэп. ISBN 0-448-01551-X.
- ^ Аткинс, Ирен Кан. Монти Холл . Нью-Йорк: Американский еврейский комитет, Библиотека устной истории, 1976.
- ^ a b c d e «Профиль Монти Холла» . filmreference.com . Проверено 26 августа 2016 года .
- ^ Knelman, Мартин (7 октября 2009). «Как Монти Холл заключил сделку со славой» . Звезда . Торонто . Проверено 13 мая 2010 года .
- ^ «Средняя школа Св. Иоанна достигает 100» . CBC News. 18 июня 2010 г.
- ^ a b c «Знаменитый Виннипеггер Монти Холл скончался в 96 лет; Холл стал соавтором Let’s Make a Deal, который дебютировал на NBC в 1963 году и стал основным продуктом телевидения» . CBCnews . CBC / Радио-Канада. Канадская пресса. 30 сентября 2017 года.
- ^ «Канадский ведущий игрового шоу Монти Холл умирает в 96 — Развлечения и Шоу-бизнес от новостей CTV» . www.ctvnews.ca .
- ^ a b c d «Монти Холл» . Архив американского телевидения . Фонд Академии телевизионных искусств и наук. 2013.
- ^ a b c d «Хозяин« Давайте заключим сделку », Монти Холл, умер в 96 лет» . Канал Fox News. 30 сентября 2017 года . Проверено 30 сентября 2017 года .
- ^ «Коммуникаторы монитора» . Архивировано из оригинала на 11 мая 2008 года . Проверено 22 мая 2008 года .
-
^ «Звуки монитора NBC» . Проверено 9 января 2015 года .
Морган Битти и Монти Холл ведущие Monitor ’58 «,» Монти Холл и Боб Уилсон ведущие Monitor ’59
- ^ Halligan, Джон. «В центре внимания выпускников» . Архивировано из оригинала 17 апреля 2007 года . Проверено 8 июня 2007 года .
- ^ a b c d «Монти Холл, создатель и ведущий« Let’s Make A Deal », умер в возрасте 96 лет» . Нью-Йорк Таймс . 30 сентября 2017 года . Проверено 1 октября 2017 года .
- ^ a b c d e Нирен, Эрин (30 сентября 2017 г.). «Монти Холл, ведущий программы ‘Let’s Make A Deal’, умер в возрасте 96 лет» . Разнообразие . Проверено 30 сентября 2017 года .
- ^ a b Трансляция канала CBS «Давайте заключим сделку» 5 октября 2009 г.
- ^ Эльбер, Линн. «Некрологи Монти Холл, ведущий и соавтор давнего телевизионного шоу« Давайте заключим сделку », умер в возрасте 96 лет» . Вашингтон Пост . Проверено 1 октября 2017 года .
- ^ «Аллея звезд Палм-Спрингс» . Архивировано из оригинального 13 октября 2012 года . Проверено 9 января 2015 года .
- ^ «Аллея славы Канады — призывники 2002 г.» . Проверено 9 января 2015 года .
- ^ «Монти Холл получает награду в Эмми» . Виннипег. Свободная пресса . 11 июня 2013 . Проверено 17 июня 2013 года .
- ↑ Marble, Steve (7 июня 2017 г.). «Мэрилин Холл, удостоенная премии« Эмми »продюсер и жена ведущего игрового шоу Монти Холла, умирает в возрасте 90 лет» . Лос-Анджелес Таймс . Проверено 16 января 2018 года .
- Рианна Коулман, Лаура (26 декабря 2014 г.). «Старейшины Беверли-Хиллз: Мэрилин и Монти Холл — победители Эмми, покровители» . Курьер Беверли-Хиллз . XXXXIX (51): 1 . Проверено 9 января 2015 года .
- ^ Торок, Райан (30 сентября 2017). «Монти Холл, филантроп и ведущий программы« Давай заключим сделку », умер в возрасте 96 лет» . Еврейский журнал .
- ^ Selvin, Стив (февраль 1975a). «Проблема в вероятности (письмо в редакцию)». Американский статистик . 29 (1): 67. JSTOR 2683689 .
- ^ Selvin, Стив (август 1975b). «О проблеме Монти Холла (письмо в редакцию)». Американский статистик . 29 (3): 134. JSTOR 2683443 .
- ^ Вос Савант, Мэрилин (9 сентября 1990 г.). «Спросите Мэрилин» . Parade Magazine : 16. Архивировано из оригинала 21 января 2013 года . Проверено 2 октября 2017 года .
- ^ Вос Савант, Мэрилин (2 декабря 1990b). «Спросите Мэрилин» . Parade Magazine : 25. Архивировано из оригинала 21 января 2013 года . Проверено 2 октября 2017 года .
- ^ a b Тирни, Джон (21 июля 1991 г.). «За дверями Монти Холла: загадка, дебаты и ответы?» . Нью-Йорк Таймс . Проверено 11 января 2017 года .
- Перейти ↑ Gruber, Gary R. (2010). 200 самых сложных головоломок в мире: головокружительные головоломки, проблемы и любопытные вопросы для оттачивания вашего мозга . Naperville, Иллинойс: Sourcebooks, Inc . Проверено 1 мая 2011 года .
JavaScript[править]
Можно просто вставить в файл monty-hall.html и открыть в браузере
<html>
<head>
<script type="text/javascript">
function getCarDoors()
{
var doors = , , ];
var carIn = Math.floor(Math.random() * 3);
doorscarIn = 1;
return doors;
}
function game(tries)
{
var res =
{
changedAndWon ,
changedAndLost ,
keepAndWon ,
keepAndLost
};
for (j = ; j < tries; j++)
{
var d = getCarDoors();
var myChoice = Math.floor(Math.random() * 3);
var changeChoice = Math.floor(Math.random() * 2) == 1;
var otherOpen;
var otherClosed;
var opened = false;
for (i = ; i < 3; i++)
{
if (i != myChoice && di == && !opened)
{
otherOpen = i;
opened = true;
}
else if (i != myChoice)
{
otherClosed = i;
}
}
var selected = changeChoice ? otherClosed myChoice;
if (dselected])
{
if (changeChoice)
res.changedAndWon++;
else
res.keepAndWon++;
}
else
{
if (changeChoice)
res.changedAndLost++;
else
res.keepAndLost++;
}
}
return res;
}
function presentGame(count, divId)
{
var res = game(count);
var changeOkProb = res.changedAndWon ((res.changedAndLost + res.changedAndWon) > ? (res.changedAndLost + res.changedAndWon) 1);
var keepOkProb = res.keepAndWon ((res.keepAndWon + res.keepAndLost) > ? (res.keepAndWon + res.keepAndLost) 1);
var text = "<tr><td>Количество попыток: " + "</td><td><b>" + count + "</b></td></tr>";
text += "<tr><td>Не изменил решение и выиграл: " + "</td><td>" + res.keepAndWon + "</td></tr>";
text += "<tr><td>Не изменил решение и проиграл: " + "</td><td>" + res.keepAndLost + "</td></tr>";
text += "<tr><td>Изменил решение и выиграл: " + "</td><td>" + res.changedAndWon + "</td></tr>";
text += "<tr><td>Изменил решение и проиграл: " + "</td><td>" + res.changedAndLost + "</td></tr>";
text += "<tr><td>Вероятность выиграть, при изменении решения: " + "</td><td>" + "<b>" + (Math.round(changeOkProb * 10000) 100) + "%</b>" + "</td></tr>";
text += "<tr><td>Вероятность выиграть, без изменения решения: " + "</td><td>" + "<b>" + (Math.round(keepOkProb * 10000) 100) + "%</b>" + "</td></tr>";
document.getElementById(divId).innerHTML = "<table>" + text + "</table>";
}
</script>
</head>
<body>
<h1>Парадокс Монти Холла</h1>
Количество попыток
<input type="text" value="100" id="tries" />
<input type="button" value="Запустить" onClick="presentGame(document.getElementById('tries').value, 'data');" />
<br />
<div id="data"></div>
</body>
</html>